Здесь: – переход; O – место
Иногда функцию инцидентности F как компоненту сети Петри представляют в виде двух функций: PRE: P´T ®
í0,1ý, POST : T´P> {0,1}.
Из вершины pÎP в вершину tÎT дуга ведет тогда и только тогда, когда PRE(p, t) = 1, а из вершины tÎT в вершину pÎP тогда и только тогда, когда POST (t, p) = 1. Разметка изображается точками в местах.
Разметка сети позволяет описывать ее состояние. Функционирование сети Петри происходит посредством перехода от одной разметки к другой. Изменение разметок происходит вследствие срабатывания переходов. Переход t может сработать, если для него выполнено условие
"p (M(p) – PRE (p, t) ? 0),
где M – текущая разметка. В нашем примере такому условию удовлетворяют переходы t1 и t2. Срабатывание перехода t приводит к изменению разметки: входные места перехода теряют по одной метке, а выходные – получают по одной метке.
Разметку M сети называют достижимой из M0, если существует последовательность срабатываний переходов, в результате которой разметка сети из M0 переходит в M. Рассмотрим формальную модель программ, в основу которой положено специальное расширение сетей Петри – ПМ-сети.
Обобщенная сеть Петри – это набор (P, T, F, H, M0), где P – множество мест; T – множество переходов; F: P´T®N?{0} и H: T´P®N?{0} – функция инцидентности; M0: P®N?{0} – начальная разметка; N – множество натуральных чисел.
Определим для сетей два типа меток: плюс-метки и минус-метки, соответственно расширим область значений функции разметки: M: P®{ …, -1, 0, 1, …}. Обозначим P+ = {p| M(p)>0}, P- = {p| M (p) < 0}. Введем функционал (предикатный функционал) C: H?F®{+, -}, т. е. каждая дуга сети помечается либо плюсом, либо минусом.
Изменим в соответствии с введенными дополнениями и правила функционирования сетей. Будем считать, что одновременно в месте не могут находиться плюс- и минус-метки. В связи с этим определим операцию аннигиляции меток, т. е. операцию одновременного уничтожения равного количества плюс- и минус-меток для одного и того же места.
Будем использовать следующие обозначения: *t = {p| F (p, t)>0}; t*=
= {p| H (t, p)>0}; *t+ (*t-) – множество таких мест, что существуют дуги из этих мест в переход и эти дуги помечены плюсом (минусом); t+*(t-*) – множество таких мест, что существуют дуги из перехода t в эти места и эти дуги помечены плюсом (минусом). Отметим, что *t+?*t- = Ø для любого t, т. е. если из места в переход существуют кратные дуги, то они должны быть помечены одним и тем же символом. Иначе из-за операции аннигиляции невозможно включение перехода t и он будет заведомо недостижим от любой начальной разметки сети.
Переход t может сработать, если для него выполнены условия:
а) для "pÎ*t+ имеет место M(p)?F(p, t),
б) для "pÎ*t- имеет место M(p)<0 и |M(p)|?F(p, t).
Срабатывание перехода t приводит к изменению разметки M на M/ по правилам:
1) если pÎt-*, то M/(p) = M(p) – H(t, p);
2) если pÎt+*, то M/(p) = M(p) + H(t, p);
3) если pÎ*t-, то M/(p) = M (p) + F(p, t);
4) если pÎ*t+, то M/(p) = M (p) – F(p, t);
5) если pÎ *t?t*, то M/(p) = M(p).
Сети, введенные выше, назовем ПМ-сетями. Проведем сравнительный анализ выразительных способностей ПМ-сетей с известными расширениями сетей Петри. Сравним семейства формальных языков, генерируемых различными классами сетей Петри.
Будем говорить, что разметка M/ достижима из M в результате последовательности срабатываний t = t1, t2 … tk, где tiÎT, 1 ? i ? k, если существует последовательность следующих друг за другом разметок:


L(N) = {?ÎT*|$M,

где T* – множество всевозможных цепочек, составленных из символов алфавита T.
Введем помечающую функцию s: T®SÈ{l}, где å – некоторый алфавит, а l – пустое слово. Функция s
легко обобщается на последовательности срабатываний gt:

Ll(N) = {s (g)|gÎL(N)} называется l-языком сети N.
Сети N1 и N2
называются эквивалентными (N1~N2), если Ll (N1) = Ll(N2). Говорят, что класс сетей ?1 мощнее класса ?2 (?2 Í?1), если для любой N2Î?2 существует N1Î?1 и N1~N2. Классы сетей ?1 и ?2 называются эквивалентными (?1~?2), если ?1Í?2 и ? 2Í?1.
Известно, что структурированные сети, приоритетные сети, сети с переключателями и дизъюнктивными правилами, ингибиторные сети эквивалентны. Докажем, что введенные здесь ПМ-сети обладают не меньшими выразительными способностями, чем отмеченные выше классы. Обозначим ?(И) – класс ингибиторных сетей, ?(ПМ) – класс ПМ-сетей.
Теорема. Имеет место следующее значение ?(И)Í?(ПМ).
Для доказательства необходимо показать, что по любой N1Î?(И) можно построить эквивалентную сеть N2Î?(ПМ).
Пусть N1 – ингибиторная сеть с начальной разметкой M0 и помечающей функцией s. Разобъем сеть N1 на n фрагментов (n – число мест в сети N1), каждый из которых включает одно место и переходы, инцидентные данному месту. Обозначим pk = {t|H(t, p)>0};


и данными переходами.
Для каждого фрагмента ингибиторной сети будем строить эквивалентный фрагмент ПМ-сети. Если исходный фрагмент не содержит ингибиторных дуг, то он остается без изменений. Если же некоторый k-й фрагмент включает хотя бы одну ингибиторную дугу, то выполняются следующие построения. В новом фрагменте будут соответственно те же переходы и то же место, что и в исходном, по-другому задаются связи между ними и разметка места.
1. Если в исходном фрагменте переход tÎ*pk, то в новом фрагменте каждой исходной дуге из t в pk будут соответствовать две дуги, ведущие из t в pk и помеченные плюсом.
2. Если в исходном фрагменте переход

3. Если в исходном фрагменте переход

4.Если в исходном фрагменте M (pk) = m, то в новом фрагменте M(pk) = = 2m-1.
 |
Рис. 8.7. Ингибиторная сеть и ПМ-сеть
После того как для каждого фрагмента ингибиторной сети построен эквивалентный фрагмент ПМ-сети, остается осуществить сочленение полученных фрагментов по переходам, помеченным одинаковыми символами. Такое построение производится на основе операции наложения. Полученное объединение фрагментов и будет являться ПМ-сетью N2, эквивалентной N1.
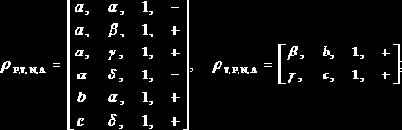 |

= (Ps, Ts,Fs, Hs, M0, s
), где


Назовем сi и di, 1 ? i ? n, выходными местами кортежа R-фрагментов. На множестве R-фрагментов кортежа можно задавать отношения, аналоги которых существуют в реальных программах. Эти отношения задаются в кортежах путем комбинаций дополнительных плюс- и минус-дуг, соединяющих переходы и места различных фрагментов. Пример одного из таких отношений будет рассмотрен ниже.
Будем считать, что объединение кортежей друг с другом может осуществляться лишь с помощью операции à, которая определяется следующим образом. Пусть S1 = (P1, T1, F1, H1, M0,1) и S2 = (P2, T2, F2, H2, M0,2) кортежа R-фрагментов, тогда S1à S2 – сеть S1 = (P/, T/, F/, H/, M/0), у которой P/ = P1?P2, T/ = T1?T2, H/ = H1?H2, F/ – есть объединение F1, F2 и дополнительных плюс-дуг, выходящих из некоторого подмножества выходных мест кортежа S1 и входящих во входной переход кортежа S2. Выбор подмножества выходных мест существенно зависит от отношений, задаваемых на множестве R-фрагментов. Операция à аналогично определяется для кортежа и просто перехода. Переходы, добавленные в СПМ-сеть посредством операции à, называем висячими.
СПМ-сеть определяется следующим образом:
1) кортеж R-фрагментов есть СПМ- сеть;
2) сеть, полученная из СПМ-сети добавлением к одному из составляющих ее кортежей либо кортежа, либо перехода, посредством операции à, является СПМ-сетью.
Сети Петри и их модификации могут успешно применяться в теории параллельного программирования как семантические модели структур параллельных программ, в частности для отображения безусловного уровня управления. СПМ-сети послужили основой для построения модели параллельных программ с большим количеством условных операторов. Безусловный уровень управления в такой модели может быть описан непосредственно СПМ-сетями, условный уровень задается специальными операторами-распознавателями. Каждому R-фрагменту приписан один оператор-распознаватель, связанный плюс-дугой с переходом b и минус-дугой с переходом g (смотрите определение R-фрагмента). Плюс-дуга соответствует выработке оператором-распознавателем значения "истина", минус-дуга соответствует значению "ложь". Таким образом, переход b (переход g ) может сработать, если место a содержит плюс-метку и оператор-распознаватель выработал значение "истина" ("ложь").
Информационно операторы-распознаватели, приписанные R-фрагмен-там одного кортежа, независимы и поэтому могут включаться асинхронно, что и обеспечивается структурой кортежа. Тем не менее в программах может иметь место отношение логической подчиненности этих операторов-распознавателей. Из-за этого при параллельном выполнении кортежа операторов-распознавателей срабатывание одних операторов-распознавателей с определенными результатами может сделать несущественными результаты срабатываний других операторов-распознавателей. Поэтому выполнение последних необходимо либо прервать, либо запретить их включение, если они еще не включались, либо уничтожить результаты их работы, если они уже выполнялись. Это обеспечивается заданием дополнительных плюс- и минус-дуг, соединяющих соответствующие переходы и места различных фрагментов.
Например, пусть выполнение оператора-распознавателя, приписанного Ri-фрагменту, несущественно, если оператор-распознаватель, приписанный Rj-фрагменту, выработал значение "истина". Тогда соединяем переход bj минус-дугой с местом ai, что позволит не включать фрагмент Ri (так как произойдет аннигиляция плюс- и минус-меток), либо, если он уже сработал, сделать разметку его выходных мест нулевой (так как сработает либо переход ai, либо переход di). Таким образом, в данном случае отношение логической подчиненности операторов-распознавателей задает соответственно и отношение на множестве R-фрагментов кортежа.
Подводя итог приведенным выше рассуждениям, можно определить модель параллельных программ как набор R = (W, S, Y, L), где
1) W – множество ячеек памяти (переменных);
2) S – безусловный уровень управления модели, представленный СПМ-сетью с заданными, если необходимо, отношениями (в частности, логической подчиненности) на множествах R-фрагментов кортежей. (Отметим, что места СПМ-сетей можно рассматривать как ячейки памяти специального вида – управляющей памяти W/, причем можно считать, что W/?W = Æ);
3) g – условный уровень управления, заданный операторами-распознавателями, являющимися предикатными термами над W; при этом операторы-распознаватели можно рассматривать как связующее звено между памятью W и управляющей памятью W/
, поскольку входными переменными для них являются элементы из из W, а свои результаты они помещают в W/.
4) L – множество цепочек операторов-преобразователей. Входные и выходные переменные операторов-преобразователей принадлежат множеству W. Мощность множества L равна числу висячих переходов в соответствующей СПМ-сети, поскольку каждому висячему переходу приписывается
одна цепочка операторов-преобразователей из L.
