Язык диспозиций
Определим некоторый класс формальных описаний задач, которые будут включать в себя как основные известные определения алгоритмов, так и некоторые неалгоритмические описания. Последние отличаются от алгоритмических тем, что в них, кроме предписаний выполнить данное преобразование текста по некоторому правилу, используются также разрешения выполнять некоторые преобразования. Такие схемы описания задач будем называть диспозициями. Предписание является вырожденным случаем разрешения, когда разрешается только одно преобразование.
Будем задавать диспозицию D знаковой системой S, множеством операторов M = {A1, A2, ..., An} (в дальнейшем оно предполагается конечным) и графом диспозиции Г(D). Каждый оператор Ai имеет один вход и Pi выходов (S1, S2, ... , SРi). Оператор Ai осуществляет некоторое преобразование Ai текстов в знаковой системе S и проверяет серию условий w0i, w1i, ... , wki. Когда оператор Ai применяется к тексту T, он проверяет, удовлетворяет ли текст T серии условий
w0i, w1i, ... , wki, и преобразует текст T по правилу Ai в текст T¢. Особую роль играет условие w0i, которое будем называть условием применимости оператора Ai. Если оно выполняется (w0i = 1), то оператор работает, как было описано выше. Иначе (т. е. если w0i = 0) оператор Ai оставляет текст неизменным (т. е. T¢ = T). Для каждого оператора Ai задается Pi функций:
j1i (w0i, w1i, ... , wki);
j2i (w0i, w1i, ... , wki);
. . .
jРii (w0i, w1i, ... , wki).
Каждая из этих функций может принимать два значения: 1 (возможно) и 0 (невозможно). Будем называть систему функций правильной, если для каждой функции существует, по крайней мере, один набор значений аргументов, при котором она принимает значение 1.
Графом диспозиции Г(D) будем называть связный граф, вершинам которого сопоставлены либо операторы диспозиции D, либо знак #. Вершины обладают следующими свойствами:
· имеется только одна вершина, называемая входом диспозиции, и обозначается aвх;
· имеется, по крайней мере, одна вершина, из которой не исходит ни одна дуга и которой сопоставлен знак #. Эти вершины называются выходами диспозиции и обозначаются aвых1, aвых2, ..., aвыхn;
· вершинам, которые не являются выходами, сопоставлены операторы диспозиции. При этом, если из вершин исходит n дуг, то ей может быть сопоставлен только тот оператор Ai, число выходов которого Pi ³ n. Каждый выход оператора Ai сопоставляется одной из дуг, исходящих из соответствующей вершины a. Каждой дуге, исходящей из a, должен быть сопоставлен, по крайней мере, один из выходов оператора Ai.
Граф Г(D) и соответствующую ему диспозицию D назовем правильными, если выполняются следующие дополнительные требования:
· из любой вершины графа Г существует путь, по крайней мере, в
один выход;
· для каждой вершины графа Г существует путь, ведущий из входа в
эту вершину.
Так определенная диспозиция задает систему допустимых последовательностей преобразований текста, а именно: если задан начальный текст T0, то оператор, сопоставленный входу диспозиции aвх, проверяет условие w0 i; если оно не выполнено (w0 i = 0), то текст T0 не меняется; если же w0 i = 1, то к тексту T0 применяется преобразование, соответствующее данному оператору, причем до выполнения этого преобразования вычисляются значения w1i, w2i, ... wki. После преобразования текста вычисляются значения функций
j1i, j2i, ..., jрii.
Те функции jj, которые принимают значение 1, определяют дуги, исходящие из входной вершины графа диспозиции, по которым возможен переход в следующую вершину. Один из этих переходов должен быть осуществлен. Тем самым на следующем шаге процесса реализации диспозиции выбирается одна из смежных с предыдущей вершина графа Г(D).
Если все функции jj = 0, то процесс останавливается. Эта ситуация называется безрезультатной остановкой.
Оператор диспозиции, сопоставленный этой вершине, применяется к полученному тексту таким же образом, как входной оператор применяется к исходному тексту T0.
Если этой вершине сопоставлен знак #, то процесс на этом заканчивается, и образовавшийся к этому моменту текст считается результатом диспозиции.
Одному и тому же начальному тексту может соответствовать несколько результатов (если один, то диспозиция однозначна).
Диспозиция называется алгоритмической, если для любого начального текста на каждом шаге возможен (а следовательно, и предписан) переход только к одной вершине графа Г(D).
Заметим, что алгоритмическая диспозиция еще не обязательно есть алгоритм, так как сами преобразования могут быть определены неоднозначно (например, марковские подстановки без указания на то, какое вхождение слова берется). Мы уже использовали понятие “реализация диспозиции”, описывая, как диспозиция преобразует исходный текст. Определим реализацию диспозиции D формально.
Будем рассматривать в графе Г(D) пути (называемые сквозными), состоящие из последовательности вершин:
al0 = aвх, al1, ..., aln, aln+1 = aвыхj,
так как ali ®










Знак ® означает: поставлен в соответствие.
Иногда удобнее описывать метод решения ряда задач как диспозицию, а затем уже тем или иным способом переходить к алгоритмам решения этих задач. Чтобы выделить алгоритмические диспозиции, следует рассматривать только такие наборы M операторов, что для " Ai Î M не более чем одна из функций j1i, j2i, ..., jрii принимает значение 1 вне зависимости от набора значений аргументов.
Пример. Рассматриваются слова в алфавите Z. Задан список слов П в алфавите Z. Слово B называется возможной основой слова C, если последнее может быть представлено в виде
D1 D2 ... DnB,
где n ³ 0 и "i (Di Î П.
Требуется для каждого слова найти все его возможные основы. Пусть
Z = {a, b, c, d}, Z¢ = {Z È ®} и П = {a, ab, ba}.
Тогда возможными основами слова abacd будут слова abacd, bacd, acd, cd, а слова babcd – слова babcd, abcd, bcd, cd.
Построим диспозицию для решения этой задачи:
M = {A1, A2, A3, A4, A5}.
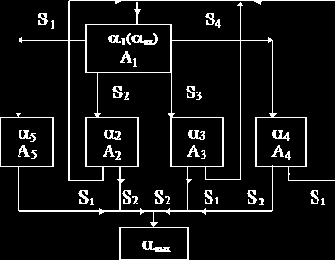 |
Рис. 10.2. Граф-схема диспозиции
Оператор A1
приписывает к исходному слову слева букву ®. Операторы A2, A3, A4 отделяют от слова, к которому они применяются, соответственно префиксы a, ab и ba (вместе с начальной буквой ®). Описание операторов находится в табл. 10.1.
